@markdown
# Softmax Regression
____
- Logistic Regression은 Binary classification이었다면, Softmax Regression은 Multinomial classification이다.
- Multinomial classification 역시 여러 개의 Binary classification으로 구성된 개념이다.
- 각각의 독립적인 Binary classification으로 분류하는 것
- Sigmoid 함수의 일반화된 형태로, 각 클래스에 대한 확률을 얻을 수 있다.
## Softmax Function
____

- 기존의 hypothesis에서 사용했던 WX 행렬 곱의 형태 Y값이 H(x)인 예측값인 것이다.

- WX의 결과에 Sigmoid를 사용하는 이유는 예측하는 ̄값이 실수가 나오기 때문이다.
- 위의 수식에 따라 WX를 계산한 각 클래스에 대한 값 H(x) (ȳ(x))이 나오게 된다.
- 각 A, B, C에 대한 계산 과정이 하나의 Binary classification이다.

- 이 값을 Softmax function에 입력해 각 클래스에 대한 확률을 얻게 된다.
- 각 확률값은 0~1사이의 값을 가지고, 이들의 총합은 1이 된다.
## Softmax Cost Function
____
- Softmax 함수로 부터 예측하고 정규화된 값을 통해 실제 값과 비교한 차이를 최소화 해야한다.
- 최소화하기 위해 `Cross-Entropy`를 사용해 차이를 줄인다.
- entropy : 어떤 확률 분포에 담긴 불확실성의 척도(정보량의 차이)

- S(Y)는 Softmax 함수가 예측한 값, L = Y는 실제값(labeled된 값)
- D는 예측한 값과 실제 값의 거리를 계산해, entropy가 감소하는 방향으로 진행하며 최저점를 만난다.
## Cross-Entropy 계산 과정
____
- 각 element간의 `Element-wise multiplication` 계산으로 최소화 할 수 있는 cost 값을 구한다.
- Li x -log(yi) 식이 element 간의 곱

- `Element-wise multiplication` : 각 element간의 곱(1x1과 1x1의 곱셈)
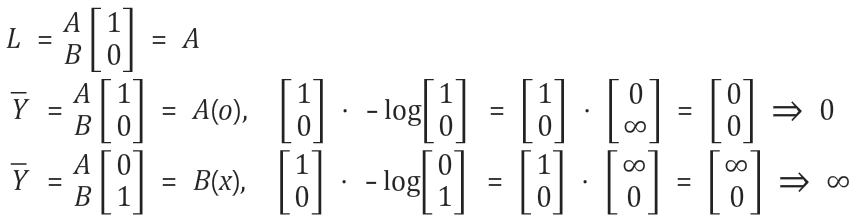
- 문자를 예측하는 학습 모델이라 가정 했을 때, 실제 값은 A이다.
- 첫번째 예측한 문자가 A일때, log(H(x))를 거쳐 0~1 사이의 값이 나오고, 계산 결과 0으로 이상적인 cost 값을 구했다.
- 두번째 예측한 문자가 B일때, log(H(x))를 거쳐 0~1 사이의 값이 나오고, 계산 결과 무한대로 잘못된 cost 값을 구했다.
#### 최종 Cross-Entropy cost function

- 최종 cost function의 결과값을 경사하강법을 사용해 minimize 한다.
그리고 최종 결과값이때 가장 큰 확률값을 가지는 것만 1로 하고 나머지는 0으로 만드는 one hot encoding 방식을 사용한다.
## Softmax Regression 구현
____
#### hypothesis - tf.nn.softmax(tf.matmul(X, W)+b)
- tf.arg_max를 활용해 확률값의 가장 높은 값을 찾아 해당 label을 리턴해준다.
<pre><code class="python" style="font-size:14px">import tensorflow as tf
x_data = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
# y data는 실제값이므로 1과 0으로 `one-hot encoding`으로 표현
y_data = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[1, 0, 0],
[1, 0, 0]]
# X, Y 변수 선언
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
#레이블의 갯수, class의 갯수를 표현
nb_classes = 3
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# 텐서플로우의 softmax 함수를 사용해 가설 정의
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
print('-------학습 시작-------')
# 이 구문은 session 사용 후 자동으로 close 해준다.
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
print('-------테스트 시작-------')
# 학습이 끝난 모델에 테스트 데이터 입력(agr_max로 확률이 가장 높은 label을 찾아줌)
a = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9]]})
print(a, sess.run(tf.arg_max(a, 1)))
b = sess.run(hypothesis, feed_dict={X: [[1, 3, 4, 3]]})
print(b, sess.run(tf.arg_max(b, 1)))
c = sess.run(hypothesis, feed_dict={X: [[1, 1, 0, 1]]})
print(c, sess.run(tf.arg_max(c, 1)))
print('-------실행 결과-------')
all = sess.run(hypothesis, feed_dict={
X: [[1, 11, 7, 9], [1, 3, 4, 3], [1, 1, 0, 1]]})
print(all, '\n------- 예측 label-------\n', sess.run(tf.arg_max(all, 1)))
</code></pre>
<pre><code class="python" style="font-size:14px">실행결과
-------학습 시작-------
0 2.86969
200 0.602141
400 0.493048
600 0.399828
800 0.30956
1000 0.235756
1200 0.212987
1400 0.194592
1600 0.179027
1800 0.165691
2000 0.154144
-------테스트 시작-------
[[ 5.30494750e-03 9.94684398e-01 1.06588586e-05]] [1]
[[ 0.85162443 0.12692477 0.02145081]] [0]
[[ 1.36959022e-08 3.37928039e-04 9.99662042e-01]] [2]
-------실행 결과-------
[[ 5.30494750e-03 9.94684398e-01 1.06588586e-05]
[ 8.51624429e-01 1.26924768e-01 2.14508064e-02]
[ 1.36959022e-08 3.37928039e-04 9.99662042e-01]]
------- 예측 label-------
[1 0 2]
</code></pre>
- `1.38904958e-03` `9.98601854e-01` `9.06129117e-06` 결과 값 중 가운데 값이 `0.9`를 나타내므로 가장 큰 값이다. 따라서 arg_max에서 이 값을 찾아 Label 1을 리턴해준다.
- softmax 함수로 학습한 모델의 실행결과 테스트 데이터에 대한 확률값과 1, 0, 2의 값을 예측한 label 값이 출력된 것을 확인 할 수 있다.
> 소스코드 - 모두를 위한 머신러닝 김석훈 교수님 강의 참고 : ([https://hunkim.github.io/ml/](https://hunkim.github.io/ml/))
'Deep Learning' 카테고리의 다른 글
| TensorFlow - Learning Rate, Data Preprocessing, Overfitting (0) | 2017.08.01 |
|---|---|
| TensorFlow - Softmax Regression(2) (0) | 2017.07.13 |
| TensorFlow - Logistic Regression(로지스틱 회귀) (0) | 2017.07.09 |
| TensorFlow - Multi Variable Linear Regression(다중 선형회귀) (0) | 2017.07.08 |
| TensorFlow - Linear Regression(선형 회귀) (0) | 2017.07.06 |