@markdown
# TensorFlow Linear Regression
<br/>
## Linear Regression(선형회귀)
____
- 통계학에서, 선형 회귀(linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다.
- 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.
- 선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링하며, 알려지지 않은 파라미터는 데이터로부터 추정한다. 이렇게 만들어진 회귀식을 선형 모델이라고 한다.(위키백과 참고)
- 예) 공부 시간 대비 시험 점수 관계, 아파트 가격과 아파트 평수, 위치, 층 등의 상관 관계
<br/>
## Supervised Learning(지도 학습)
____
- 지도 학습은 훈련 데이터로 부터 하나의 함수를 유추해내기 위한 머신러닝의 한 방법
- 주어진 training data set을 가지고 학습을 시키는 개념
- 회귀(Regression)가 대표적인 지도학습
- 예) labeled 된(답이 정해진 것) 동물 사진을 학습 시키는 것, AlphaGo에게 사람의 바둑 기보를 학습 시키는 것
<br/>
## TensorFlow의 비용 함수(Cost Function)
____
- 입력 데이타 x_data를 이용해, y_data를 만들 수 있는 최적의 W와 b를 찾는데 목적이 있다.
- cost function은 W와 b 값이 실제 y 값과의 차이를 줄여주는 것이 목적
- 데이터 셋의 값들을 반복해서 적용하고, 학습 시키면서 최적의 W와 b를 업데이트 시킨다.
<br/>
## TensorFlow Gradient Descent(경사 하강법)
____
- Cost function의 최소값을 찾는 알고리즘이 옵티마이저인데, 이번 단순 선형 회귀에서는 경사 하강법을 사용한다.
- 경사 하강법은 Cost function의 곡선을 미분한 기울기를 사용해 최소값을 찾는다.
- 구해진 곡선의 기울기에 따라 점점 하강하면서 최소값을 찾는 것이다.
<br/>
## TensorFlow 구현 단계
____
### 준비 단계
- 데이터 셋, 사용할 TensorFlow 변수 선언, 가설 설정, cost function 정의
### 학습 단계
- 데이터 셋 `x_data`와 `y_data`을 넣어 경사하강법에 의해 Cost function이 최소가 되는 W와 b를 구한다.
- 이 단계에서 W값을 변화시키면서 반복적으로 x_data로 계산을 하여, 실제 측정 데이터와 가설에 의해서 예측된 결과값에 대한 차이를 찾아내고 최적의 W와 b값을 찾아낸다.
### 예측 단계
- 학습 단계에서 찾아낸 W와 b를 사용하여 학습된 모델로 결과 값을 예측한다.
- `x_data`에 임의이 값을 입력해 예측된 데이터를 리턴 받는다.
<br/>
## TensorFlow의 단순 선형 회귀
____
- 김석훈 교수님 강의에 있는 시험점수 상관관계 예제를 구현한 것
(강의 링크 -> [모두를 위한 딥러닝 강좌](https://www.youtube.com/playlist?list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm))
- 공부 시간과 시험 점수의 관계식
- x : 공부시간, y : 시험점수, b : 보정값
- 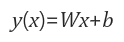
<br/>
## TensorFlow Variable 사용한 단순 선형회귀 학습
<pre><code class="python" style="font-size:14px">import tensorflow as tf
# X and Y data
x_train = [1, 2, 3]
y_train = [2, 4, 6]
# TensorFlow 변수 사용, Trainable 한 값(학습 중에 변경할 수 있는 값)
# 값이 하나인 1차원 Array Shape을 가지는 것을 선언
W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# 가설(graph 만들기) y = Wx + b
hypothesis = x_train * W + b
# cost/loss 함수
cost = tf.reduce_mean(tf.square(hypothesis - y_train))
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
# 옵티마이저로 cost 함수를 최소화 하겠다는 것, TensorFlow에서 학습하면서 알아서 W와 b를 조절하여 최소화한다.
train = optimizer.minimize(cost)
# TensorFlow를 시작하는 세션을 지정
sess = tf.Session()
# TensorFlow 변수들 초기화
sess.run(tf.global_variables_initializer())
# 위에서 세운 가설(graph)를 1001번 학습 시켜 W와 b값을 찾는다
for step in range(1001):
# 학습이 일어나는 시점
sess.run(train)
if step % 100 == 0:
print(step, sess.run(cost), sess.run(W), sess.run(b))
</code></pre>
<pre><code class="python" style="font-size:14px">실행결과
step cost W b
0 12.7923 [ 0.84884512] [-1.14861417]
100 0.0256671 [ 2.18606234] [-0.42299327]
200 0.0158607 [ 2.14627051] [-0.33250722]
300 0.00980095 [ 2.11498189] [-0.26138118]
400 0.00605636 [ 2.09038615] [-0.20546943]
500 0.00374246 [ 2.0710516] [-0.16151728]
600 0.00231261 [ 2.05585289] [-0.12696703]
700 0.00142906 [ 2.04390574] [-0.09980786]
800 0.000883068 [ 2.03451371] [-0.07845809]
900 0.000545674 [ 2.02713084] [-0.061675 ]
1000 0.000337201 [ 2.02132726] [-0.04848217]
- 학습 할수록 cost 값이 줄어들고 b 값이 0으로 수렴하는 것을 확인 할 수 있다.
</code></pre>
<br/>
## TensorFlow placeholder 사용한 단순 선형회귀 학습
_____
<pre><code class="python" style="font-size:14px">import tensorflow as tf
W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
X = tf.placeholder(tf.float32, shape=[None])
Y = tf.placeholder(tf.float32, shape=[None])
# 가설 설정 XW+b
hypothesis = X * W + b
# cost function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# 경사하강법을 사용한 최소화
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
cost_val, W_val, b_val, _ =
sess.run([cost, W, b, train], feed_dict={X: [1, 2, 3], Y: [2, 4, 6]})
if step % 200 == 0:
print(step, cost_val, W_val, b_val)
</code></pre>
<br/>
### 학습시킨 모델에 데이터 입력
- 입력 데이터의 2배 값인지 예측하는 모델
<pre><code class="python" style="font-size:14px">print(sess.run(hypothesis, feed_dict={X: [5]}))
print(sess.run(hypothesis, feed_dict={X: [2.5]}))
print(sess.run(hypothesis, feed_dict={X: [1.5, 3.5]}))
</code></pre>
<pre><code class="python" style="font-size:14px">[ 9.9869194]
[ 4.99891186]
[ 3.00370908 6.99411488]
실행결과 입력 데이터 x 값의 2배를 예측하는 것을 확인 할 수 있다.
</code></pre>
<br/>
'Deep Learning' 카테고리의 다른 글
| TensorFlow - Logistic Regression(로지스틱 회귀) (0) | 2017.07.09 |
|---|---|
| TensorFlow - Multi Variable Linear Regression(다중 선형회귀) (0) | 2017.07.08 |
| TensorFlow - 변수형 종류, 행렬 다루기 (0) | 2017.06.19 |
| TensorFlow - 기본 사용법 (0) | 2017.06.16 |
| TensorFlow - Windows 7 설치하기 (0) | 2017.06.15 |